
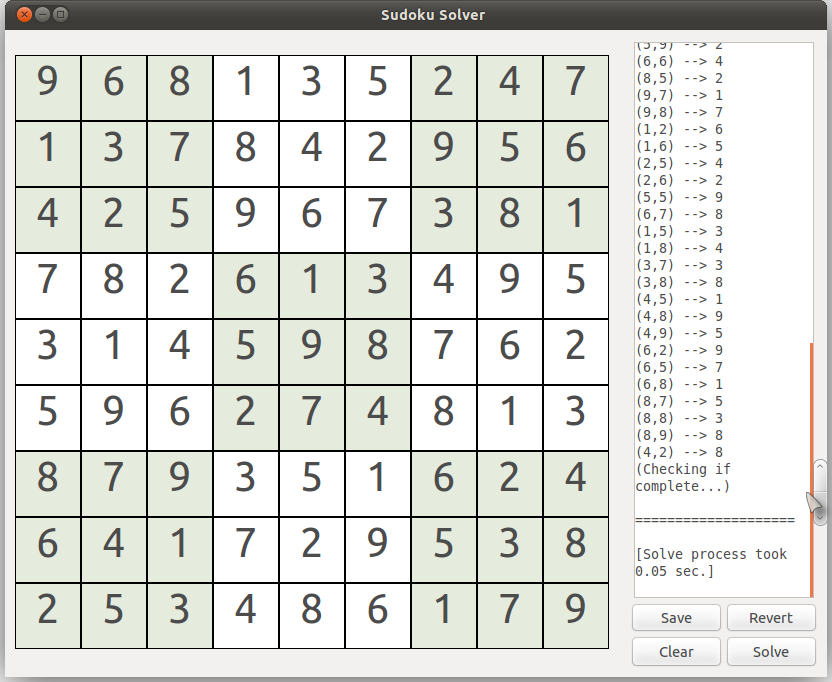
Note that this tree is a graphical representation of the process taken by the algorithm, and is not generated by the IML code. The search tree formed by the algorithm is shown below. Having failed to obtain a solution using the basic solver, the IML program then calls my modified version of Algorithm X. Running the basic solver on the puzzle at the beginning of this post yields the grid on the right. The adaptation of Algorithm X used in this post is a bit convoluted, so is only described in the context of the example puzzle above. The algorithm navigates the search tree until a solution is found, and then terminates. The algorithm forms a search tree with columns of the exact cover matrix forming the nodes of the tree and rows of the exact cover matrix forming the branches of the tree. The solver can also solve the world’s hardest Sudoku puzzles, but those puzzles are not reproduced here due to copyright.Īlgorithm X is an efficient backtracking algorithm for solving exact cover problems (Knuth, 2009).
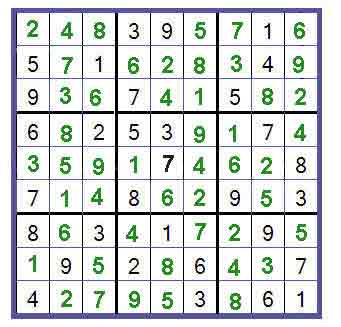
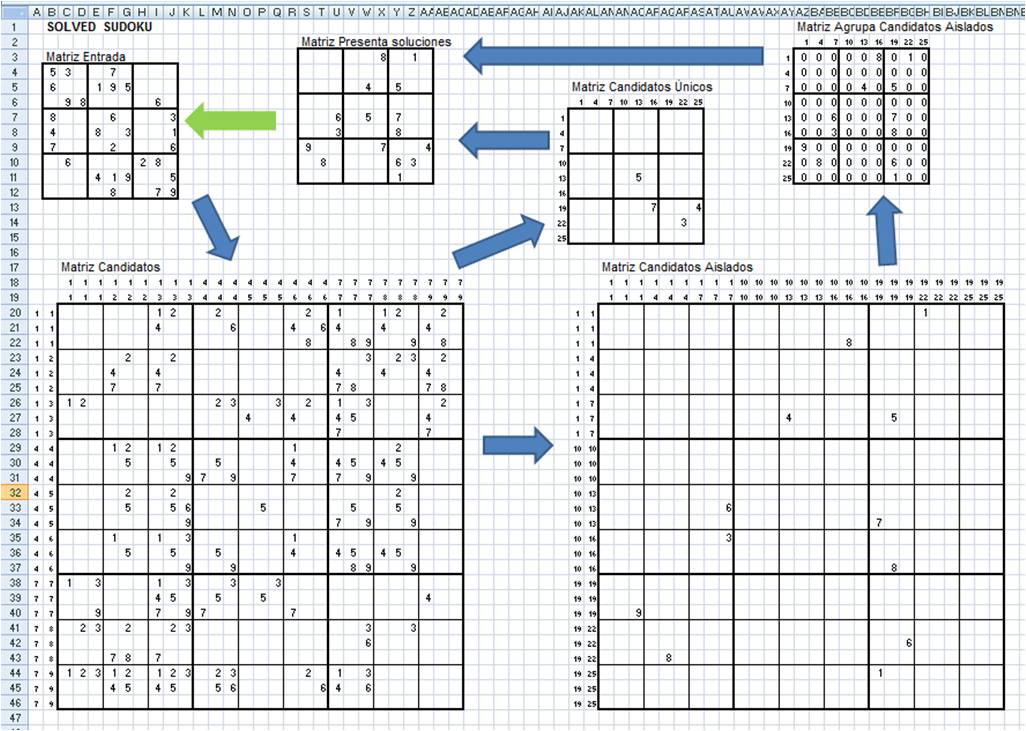
This post demonstrates how the entire puzzle can be solved through a combination of the simple solver from Part 1 and an adaptation of a backtracking algorithm called Algorithm X. The basic solver manages to solve the majority of the puzzle before giving up. The puzzle on the right was obtained from Sudoku Garden ( ) and is reproduced here in its original form under the creative commons attributions license. Unfortunately, the simple solver fails when presented with more difficult Sudoku problems. By treating Sudoku as an exact cover problem, the algorithm efficiently found solutions to simple Sudoku problems using basic logic.
Part 1 of this topic presented a simple Sudoku solver.


 0 kommentar(er)
0 kommentar(er)
